Fig. 1 from Mueller and Smola showing clusters of similar dataset columns as classified by deep neural networks.
In a new paper published earlier this month, Jonas Mueller and Alex Smola, from the research team at Amazon Web Services, propose a new method for matching unseen columns across data tables (a task known as schema matching).
Mueller and Smola's method is as elegant as it is simple: a combination of neural networks learns to produce lower-dimensional representations of columns, also known as embeddings, based on the distribution of the data contained in each column. These representations can be quickly compared to one another using standard clustering techniques, allowing the programmer to efficiently group columns that likely refer to the same data without knowing how the columns were produced.
In the following post, I'll provide some background on why schema matching is an important challenge before diving into an explanation of Mueller and Smola's approach. We'll see how their models work and think about potential applications to data cleaning and discovery more broadly beyond the specific task of schema matching.
What is schema matching?
In the context of Muller and Smola's work, schema matching refers to the task of grouping together columns in data tables that refer to the same attributes. A key challenge in this task is to infer the meaning of a column without knowing its origin. Mueller and Smola summarize the task as an effort to determine the underlying random variables represented by columns:
Given a previously-unseen data table, we aim to automatically infer what type of variable was measured to generate the observations in each column.
As a simple example, imagine a data table buildings had a column address with values like 123 MAIN ST.,
while a data table people had a column street_addr with values like
5 W. 3rd Ave New York NY First Floor. A person could easily tell that these two
columns had the same semantic meaning (i.e. street addresses corresponding to each record)
but it's hard to write a computer program that can make the same judgment across
a variety of different domains and data types.
Simple approaches to schema matching, as outlined by Rahm and Bernstein
(2001), compare the names of the fields
to find matches (what Rahm and Bernstein call schema-level matching). address
and street_addr are reasonably similar strings, so we can infer that their columns
probably have similar meaning. However, this approach breaks down when the column
names are opaque, or uninformative, which is often the case in large heterogenous data stores.
In these cases, we have to consider the data contained in the column, not just
its name.
Contemporary approaches to schema matching with opaque column names typically try to compare the distributions of the data values within columns instead of (or in addition to) the names of the columns themselves. DataMade provides a nice summary of these approaches in the blog post Modern Approaches to Schema Matching (2017). Mueller and Smola's principal intervention, as we'll see, is to bring to bear neural networks to the task of comparing distributions — and to use those neural networks to cluster low-dimensional encodings of the columns instead of comparing them directly.
Neural networks and deep embeddings
The crux of Mueller and Smola's method is to train a neural network to produce embeddings based on column distributions. An embedding is a lower-dimensional vector representation of the data that encodes some type of semantic meaning that the neural network has learned to recognize. With columns converted to embeddings, they can be clustered together using fast approximate nearest neighbor algorithms, as described by Muja and Lowe (2009). Figure 1 from the paper shows a visualization of these clusters of embeddings projected into two dimensions, where the relationship between visual space and the semantic meaning of columns is clearer.
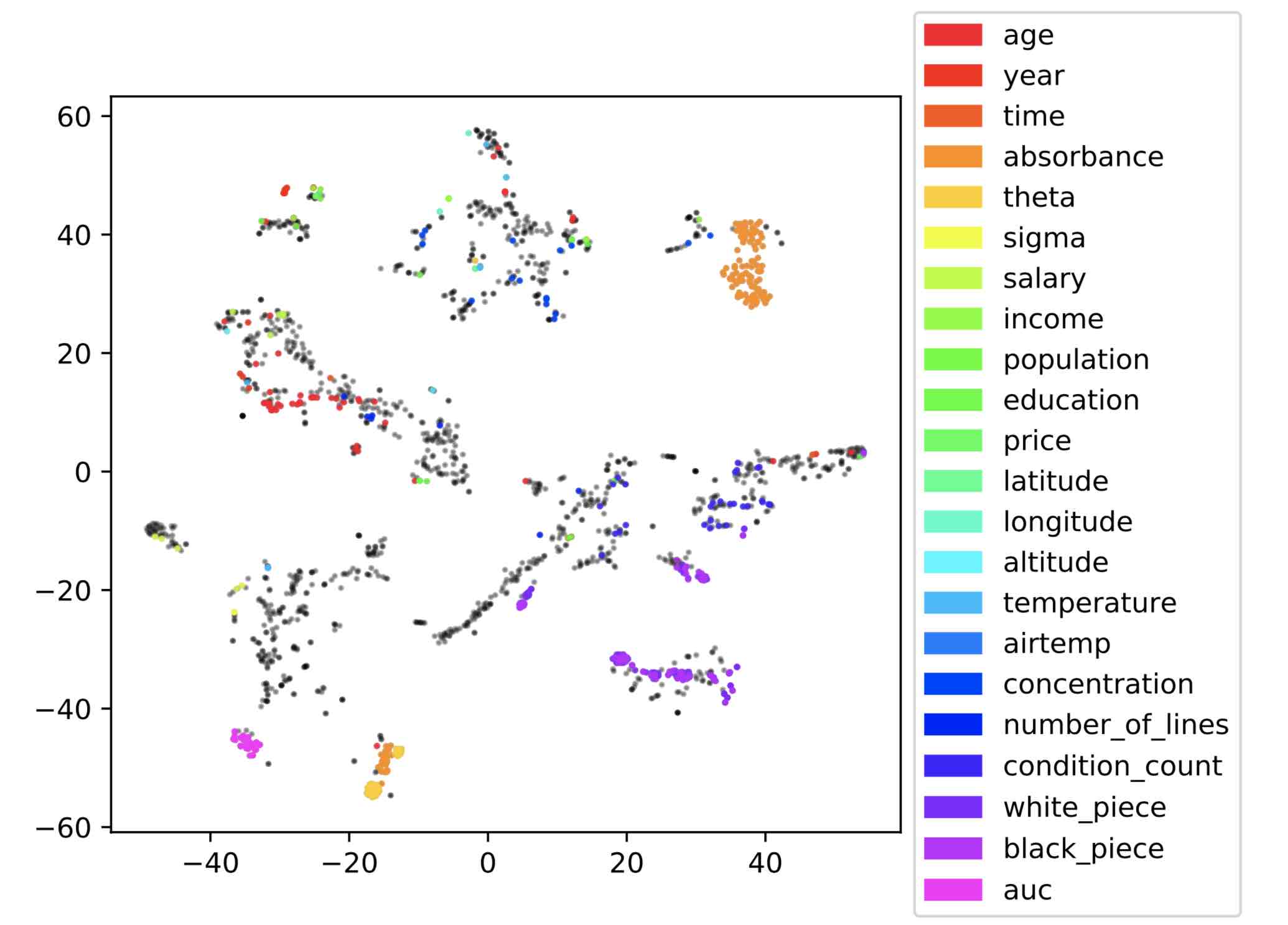
Figure 1, clustered column embeddings as visualized in two dimensions.
In Mueller and Smola's architecture, there are actually two neural networks at work: \(h_{\theta}\), which learns to produce embeddings from columns, and \(g_{\psi}\), which learns to produce an adjustment term based on how common the column's distribution is. \(h_{\theta}\) and \(g_{\theta}\) interact to produce probabilities \(p_{ij}\) that two columns \(D_i\) and \(D_j\) refer to the same variable:
Where:
Standard triaining rules apply: both \(h_{\theta}\) and \(g_{\psi}\) are trained via stochastic gradient descent, where the loss function is cross-entropy loss for binary classification.
In essence, Mueller and Smola's probabilities suggest that the degree of similarity between two columns can be thought of as the squared distance between their embeddings \((h_{\theta}(D_i) - h_{\theta}(D_j))^2\) scaled by a factor \(g_{\psi}(D_i) + g_{\psi}(D_j)\) representing how common the distributions of the columns are.
Two networks are better than one
Why train two networks? It turns out \(g_{\psi}\) adds an important element by learning to adjust for columns with common distributions.
Columns with very common sets of values, like Boolean True/False columns, will tend to produce very
high confidence matches when only their embeddings are compared. This will be
true even when the columns refer to completely different attributes: the distribution
of values in a column was_raining may look nearly identical to a column has_email,
for example, even though the columns were generated by different variables.
To address this problem, \(g_{\psi}\) learns to produce a large value in response to columns with common distributions, making them categorically less likely to match. Mueller and Smola call this value an adjustment factor and provide data from experiments showing that models lacking \(g_{\psi}\) performed much worse.
Different architectures for different data types
One major challenge facing Mueller and Smola's architecture is that the types of data represented by different columns can vary widely. Columns can contain strings, integers, floats, blocks of free text — and each of these columns needs to be legible to the networks \(h_{\theta}\) and \(g_{\psi}\).
The biggest hurdle involved in making heterogenous data legible to the networks
is that columns with different data types cannot be encoded and input into the network
in the same way. A column with a string data type, like our address column above,
needs to be encoded differently from a numeric column like price before being
converted to a vector that can pass through the networks. Another hurdle is that
networks with inputs of widely-varying magnitudes tend to train poorly, so even
if two columns are both numeric, they may have completely different ranges and
will be hard to compare as a result.
Mueller and Smola tackle the problem of heterogenous data types by training separate
networks for different data types. String columns that represent discrete English words
are converted to vector inputs using the fastText word vector embeddings,
while numeric columns are converted to 32-dimensional vectors representing the signed 32-bit binary
representation of the number. In both cases, \(h_{\theta}\) and \(g_{\psi}\) have three
fully-connected hidden layers of 300 nodes each, with ReLU activations in \(g_{\psi}\) and tanh activations in
\(h_{\theta}\), and where \(h_{\theta}\) produces a 300-dimensional vector output and
\(g_{\psi}\) produces a scalar.
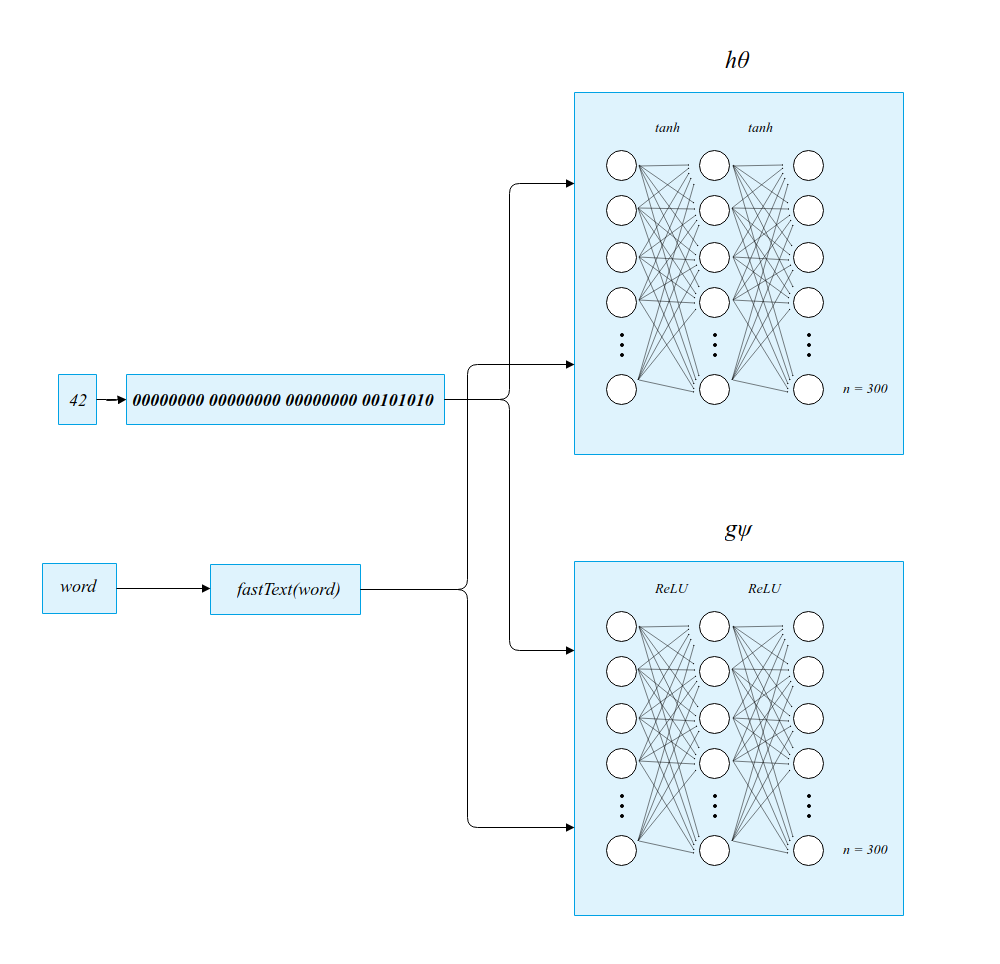
For numeric columns and simple English string columns, inputs are encoded before being passed into fully-connected networks.
What if a string column does not represent English text, and so can't be encoded
by fastText? In that case, Mueller and Smola instead take \(h_{\theta}\) and \(g_{\psi}\)
to be bidirectional character-level LSTMs.
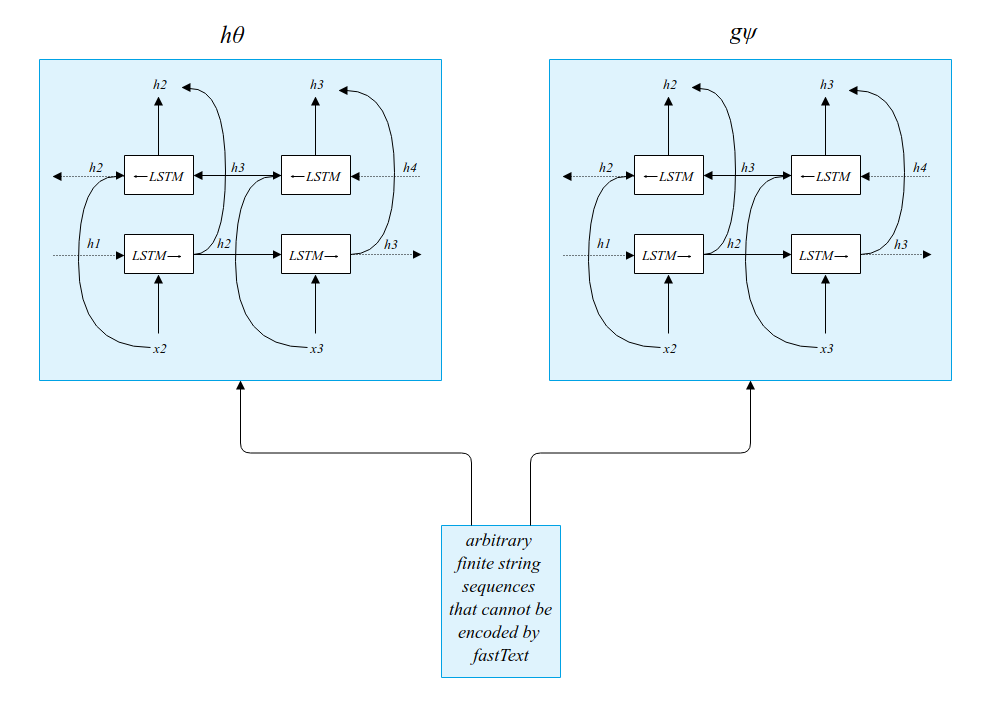
In the case of indeterminate non-English strings, inputs are passed directly into bidirectional LSTMs.
Mueller and Smola don't make it clear how the data types of each column are determined prior to encoding the input to the networks. Since the training data for the paper was generated from OpenML source data, which provides feature type metadata for each dataset, we can assume that Mueller and Smola used dataset metadata to determine the data types in each column. This metadata is unlikely to exist outside of a lab context, however, so methods of accurately approximating the data types of each column would be a necessary improvement in order to put Mueller and Smola's work into production.
Speed and generalization
While Mueller and Smola show that their network architecture outperforms other statistical classifiers on key metrics like precision, recall, and AUC, their metric results may not fully capture the potential of the approach. As their charts demonstrate, deep embeddings produce incremental improvements in most domains, and breakthrough improvement in only a few.
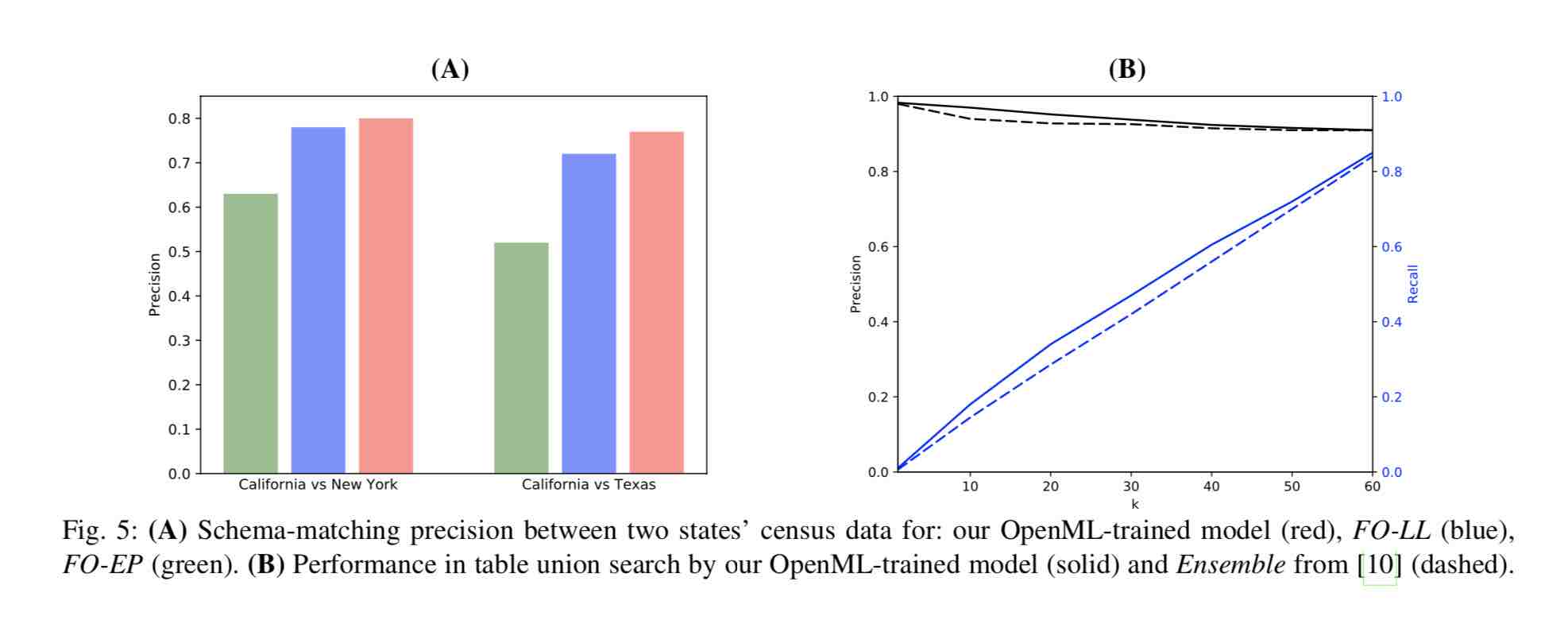
Deep embeddings seem to provide an incremental improvement in precision and recall over next-best techniques for schema matching.
As I see it, the key attractions of using deep embeddings for schema matching are speed and generalizability. In terms of speed, the architecture of the network produces a relatively fast algorithm: instead of classifying the similarity of each pair of columns, Mueller and Smola's method only requires passing each column through each network once, since grouping is performed by fast clustering algorithms. In terms of generalizability, Mueller and Smola apply the same network to multiple domains to demonstrate that it generalizes well, overcoming what they consider to be a key challenge with distributional approaches.
Mueller and Smola don't directly compare speed or generalizability across different techniques, but they seem to be important advantages of deep embeddings. I'd love to see a follow-up paper that compares different approaches based on speed and generalizability in addition to the traditional performance metrics that Mueller and Smola considered.
Potential applications beyond schema matching
As Mueller and Smola's paper demonstrates, deep embeddings have real potential as a solution for schema matching. But their paper also hints at possible applications in a number of other domains as well.
In the paper, Mueller and Smola experiment with the related task of table union search, where data tables are grouped according to whether or not they share enough columns that their rows can be sensibly stacked (or "unioned"). With embeddings, pairwise column distances merely have to be aggregated in order to produce an overall score indicating whether two tables can be unioned or not. Mueller and Smola report that the same embeddings that worked for schema matching produced slightly better results than the best-performing benchmark so far in this task.
Perhaps most exciting to me, however, is the potential application of deep embeddings to entity resolution, a problem that the DataMade team has pursued extensively through its work on Dedupe.io. The core problem of entity resolution — determining which records in a dataset refer to the same entity — is analogous to the problem of schema matching, except that entity resolution treats table rows as the fundamental unit of comparison instead of table columns. Currently, Dedupe.io classifies rows with logistic regression and clusters suspected duplicates uing a hierarchical clustering algorithm based on inferred centroids; deep embeddings could accomplish the same work, with potentially better accuracy and generalizability.
Whether generated over rows or columns in a data table, deep embeddings are an exciting development that pushes the envelope for data cleaning and discovery. I'm looking forward to putting Mueller and Smola's ideas into production soon.