Process and Procedure

One of the most enlightening parts of learning a Lisp (in my case, the lovely research dialect Scheme¹) has been getting familiar with the way that functional languages like Scheme treat recursion. Studying recursion in Scheme has helped me develop a richer understanding of the distinction between process and procedure, two different ways of imagining function execution that each help clarify how an interpreter thinks.

Form and function

Growing up on Python, I was always taught that "recursion" described functions that called themselves. Take a quick and classic example: a recursive function for adding positive integers.

def add(a, b):
    '''
    Sum positive integers `a` and `b`.
    '''
    if b == 0:
        return a
    else:
        b -= 1
        return (1 + (add(a, b)))

In all cases where b != 0, add will indeed call itself. But there's a second, more subtle property that makes add recursive: its calls to itself will expand as it executes, and the stack frame, the queue that the Python interpreter uses to monitor and execute function calls, will grow. In other words, the interpreter will keep holding on to progressively bigger versions of (1 + (add(a, b))) until it reaches the "base case" where b == 0, when it can finally start to contract on itself and perform the sequential additions that have been piling up.

To see this expansion in practice, we can use Python's built-in inspect module to peek at the stack at the moment the interpreter reaches the base case.

import inspect

def print_stack():
    '''
    Print the current stack frame in a function call.
    '''
    # Set a counter for pretty printing
    idx = 0
    for frame in inspect.stack():
        # Filter out the portion of the stack corresponding to the trace
        if frame.code_context and 'inspect' not in frame.code_context[0]:
            print(('\t' * idx) + frame.code_context[0].strip())
            idx += 1

def add(a, b):
    '''
    Sum positive integers `a` and `b`.
    '''
    if b == 0:
        # Before the execution starts contracting, print the stack
        print_stack()
        return a
    else:
        b -= 1
        return (1 + (add(a, b)))

Now the interpreter can print the stack of queued function calls, illustrating the progressive expansion of add:

>>> add(1, 5)
return (1 + (add(a, b)))
    return (1 + (add(a, b)))
        return (1 + (add(a, b)))
            return (1 + (add(a, b)))
                return (1 + (add(a, b)))
6

As add moves deeper into its recursion, the function calls pile up on one another. When it reaches the base case, the interpreter can begin to evaluate the sequence of nested expressions, which will look something like this:

(1 + (1 + (1 + (1 + (1 + (1))))))

This expansionary behavior is one reason that recursion can be dangerous in production code. As b gets larger and larger, the interpreter will have to hold all of the function calls in memory as it approaches the base case. For very large inputs, this can cause memory to run out, or cause the stack to overflow.

So from a practical perspective, there are in fact two important properties that distinguish recursive functions, one largely formal and one largely functional:

1. The function has the capacity to call itself (form)
2. The function will expand on execution until it reaches a base case (function)

Recursive procedure, iterative process

The two properties of recursive functions are handy heuristics, but there's a twist: they aren't guaranteed to go together. Sometimes, the form of the function—the way it's written for the human eye, or what I'll call its "procedure"—doesn't intuitively match the way that a given interpreter will execute it (that is, the "process," or machine instructions, that it spawns).

As an example, take a modified version of add that makes use of a slightly different recursive call:

def add_iter(a, b):
    '''
    Sum positive integers `a` and `b`, with a (potentially) iterative process.
    '''
    if b == 0:
        return a
    else:
        return add_iter((a + 1), (b - 1))

Notice the altered return statement: rather than nest the recursive call in an addition expression like (1 + add_iter(a, b)), add_iter increments and decrements a in place. Since the call to add will be the last instruction that the function executes, we can more precisely say that add is tail-recursive.

Thanks to tail-recursion, the modified add_iter appears to behave similarly to a classic for-loop. The argument a stores the state as it increments, while the argument b acts like a counter, progressively stepping towards 0. A state variable and a counter—that's a decidedly iterative relationship! When add_iter executes, then, we might expect its process to behave iteratively rather than recursively. We could imagine something like the following evaluation history, where a new stack gets created for each call:

add_iter(1, 5)
add_iter(2, 4)
add_iter(3, 3)
add_iter(4, 2)
add_iter(5, 1)
add_iter(6, 0)
6

In Python, however, it turns out that add_iter executes recursively, in the exact same fashion as add. Calling a traced version of add_iter reveals the expansion of the stack:

>>> add_iter(1, 5)
return add_iter((a + 1), (b - 1))
    return add_iter((a + 1), (b - 1))
        return add_iter((a + 1), (b - 1))
            return add_iter((a + 1), (b - 1))
                return add_iter((a + 1), (b - 1))

The interpreter doesn't really need the outer frames to keep track of where add_iter is: as in a for-loop, the state variable a and the counter b do a fine job of keeping time all on their own. But Python holds on to them anyway, producing a recursive process where an iterative one would have made more sense.

Out with the stack: tail-call optimization in Scheme

Unlike Python, Scheme doesn't hang on to the outer frames of the stack when it executes a tail-recursive function. Instead, Scheme is tail-call optimized: the interpreter figures out when it can afford to toss unnecessary stack frames in tail-recursive functions. Because tail calls are optimized in Scheme, the interpreter can execute iterative processes from recursive procedures.

Take an equivalent procedure to add_iter, implemented in Scheme. Using the built-in procedure debug, we can inspect the stack interactively at the moment when the interpreter reaches the base case:

(define (add-iter a b)
  ;; Sum `a` and `b`, iteratively.
  (if (= b 0)
      (debug) 
      (add-iter (+ a 1) (- b 1))))

Here's the output:

1 ]=> (add-iter 1 5)

There are 4 subproblems on the stack.

Subproblem level: 0 (this is the lowest subproblem level)
Compiled code expression unknown
#[compiled-return-address 13 ("rep" #x2f) #xd8 #x247d3f8]
There is no current environment.
There is no execution history for this subproblem.
You are now in the debugger.  Type q to quit, ? for commands.

There's a lot of information here! The relevant content for our purposes is the status of the subproblems on the stack.³ The interpreter reports that There are 4 problems on the stack, meaning there are four procedures that need to be evaluated in this frame. The history command H can print a summary of those subproblems:

2 debug> H
SL#  Procedure-name          Expression

0                            ;compiled code
1                            ;compiled code
2                            ;compiled code
3                            ;compiled code

Whatever the interpreter's doing, it's not hanging on to calls to add-iter.²

To see the contrast with a recursive process, we can run a version of the procedure without a tail call and see what the debugger reports:

(define (add-rec a b)
  ;; Sum `a` and `b`.
  (if (= b 0)
      (debug)
      (+ 1 (add-rec a (- b 1)))))

Here's the output:

1 ]=> (add-rec 1 5)

There are 9 subproblems on the stack.

Subproblem level: 0 (this is the lowest subproblem level)
Expression (from stack):
    (+ 1 ###)
 subproblem being executed (marked by ###):
    (add-rec a (- b 1))
Environment created by the procedure: ADD-REC

 applied to: (1 1)
The execution history for this subproblem contains 3 reductions.
You are now in the debugger.  Type q to quit, ? for commands.

The debugger reports that the interpreter is holding on to 9 procedures in this stack. Printing a summary reveals the culprit: nested calls to add-rec!

2 debug> H
SL#  Procedure-name          Expression

0    add-rec                 (+ 1 (add-rec a (- b 1)))
1    add-rec                 (+ 1 (add-rec a (- b 1)))
2    add-rec                 (+ 1 (add-rec a (- b 1)))
3    add-rec                 (+ 1 (add-rec a (- b 1)))
4    add-rec                 (+ 1 (add-rec a (- b 1)))
5                            ;compiled code
6                            ;compiled code
7                            ;compiled code
8                            ;compiled code

With optimized tail calls, the Scheme interpreter doesn't have to keep any extra data in memory other than the current values of the state variable and the counter at any given point in time during the function execution. If we design a function to use a tail call we can achieve nice and clean iteration—in the form of a recursive procedure.

Fun with recursion and iteration in Scheme

Thanks to tail-call optimization, recursive procedures are easy to re-implement as iterative processes in Scheme. Since add was a toy example, let's take on a more challenging algorithm: Pascal's triangle.

Building Pascal's triangle involves a classic recursive algorithm: to find any given element in the triangle, sum the two elements that precede it. Keep going until you reach the first element, which is 1.

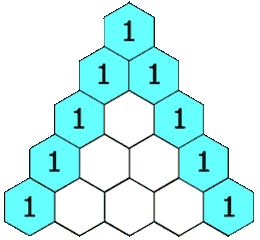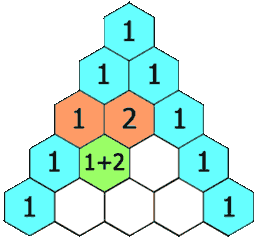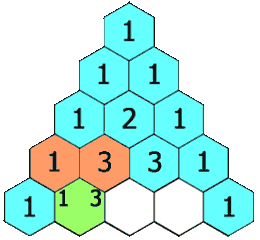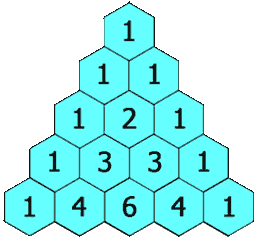
Pascal's triangle, computed up to n = 5.This animation by Wikipedia user Hersfold illustrates an iterative version of the algorithm.

Writing a recursive procedure that generates a recursive process to calculate elements in Pascal's triangle is relatively simple. There are four key insights:

1. Every element in the triangle has a row position (row) and a column position (col)
2. The value of any given element in the triangle can be computed by summing together the elements in the preceding row that have column positions col - 1 and col
3. Elements at the edge and peak of the triangle, where row = col, always have a value of 1 (the base case of the algorithm)
4. All elements with row/column positions that would seem to lie "outside" the triangle can be treated as if they have the value 0

Based on these insights, we can write a procedure that uses a recursive process to calculate the value for any given row, col position:

(define (pascal row col)
  ;;; Calculate a value in Pascal's triangle for a given row and col
  (cond ((= row col) 1)  ; Edges of the triangle
        ((or (< col 1) (> col row)) 0)  ; Ignore values beyond triangle bounds
        (else (+ (pascal (- row 1) (- col 1))  ; Preceding value on the left
                 (pascal (- row 1) col)))))    ; Preceding value on the right

Then, we can use this procedure to calculate the coefficients for any given row by iterating over the column positions in that row:

(define (binom-coef n)
  ;;; Display the binomial coefficients for `n`
  (define (pascal-row row col)
      (if (= row col)
          (write-to-string (pascal row col))
          (string-append (write-to-string (pascal row col))
                          " "
                          (pascal-row row (+ col 1)))))
  (pascal-row n 1))

A similar logic applies for the triangle itself, which we can build from the ground up.

(define (build-triangle n count)
  (if (= count n)
      (binom-coef count)
      (string-append (binom-coef count)
                     "\n"
                     (build-triangle n (+ count 1)))))

Putting it all together:

(define (pascals-triangle n)
  (display (build-triangle n 1)))

(pascals-triangle 5)
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1

There's the triangle! Unfortunately, there are at least two reasons that this solution is highly inefficient:

1. The procedure that computes the value for any given position, pascal, spawns a recursive process

2. Since pascal recurses the entire triangle every time it computes a value, the procedure winds up doing a bunch of redundant work

Luckily, an iterative process can help improve on both of these weaknesses.

Iterative Pascal

Following a similar logic as add_iter, designing a recursive procedure that spawns an iterative process to generate Pascal's triangle is a snap. Instead of recursing back down the entire triangle to compute any given value, an iterative process should instead start at the base of the triangle and work its way up.

First, we need a procedure that can take an existing row of coefficients and compute the next row in the sequence. Since each element is computed using two successive elements in the preceding row, all we have to do is treat each row as if it starts and ends with a 0 element and sum successive elements as we iterate over the row.

(define (next-row curr-coefs row)
  (cond ((null? (cdr row)) ; End of the list: make sure to append last elem
           (append curr-coefs (list (car row))))
        ((null? curr-coefs) ; Start of the list: make sure to append first elem
           (next-row (list (car row)) row))
        (else ; Sum two successive elements and move down the list
           (next-row (append curr-coefs (list (+ (car row) (cadr row))))
                     (cdr row)))))

We'll also need a procedure to convert lists to strings, so that we can print the results to the console. To avoid printing the leading and trailing zeroes, which don't actually exist in the triangle, chop the start and the end off of any given row.

(define (list-to-string str lst)
  (cond ((null? (cdr lst)) str)
        ((string=? str "") (list-to-string (string (cadr lst)) (cdr (cdr lst))))
        (else (list-to-string (string-append str " " (string (car lst))) (cdr lst)))))

Finally, we need a procedure to build up rows. The key to doing this iteratively is to recognize that we actually need two state variables: one to hold the current row as a list (lst) and one to hold the string that collates all of the lists for printing (str).

(define (build-triangle str lst n count)
  (let ((next-str (string-append str "\n" (list-to-string "" (next-row (list) lst)))))
    (if (= count n)
        next-str
        (build-triangle next-str (next-row (list) lst) n (+ count 1)))))

Putting it all together with initial values:

(define (pascal-iter n)
  ;;; Compute and display Pascal's triangle up to row `n` -- iteratively!
  (let ((init-value (list 0 1 0)))
    (display (build-triangle (list-to-string "" init-value) init-value n 1))))

(pascal-iter 5)
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1

Thinking like the interpreter

At small scales, the distinction between recursive and iterative processes doesn't make much of a difference. But as the size of the input grows without bound, the nature of the process that a procedure spawns becomes much more important: does the machine have to store ever-expanding function calls for every step of the procedure, or can it get away with only storing three arguments and an operator?

As a functional, tail-call optimized language, Scheme encourages a more sophisticated treatment of recursion than Python. Recursive procedures in Scheme can spawn processes that are either iterative or recursive, depending on the context, allowing the programmer finer-grained control over the machine execution—if they can think like the machine.⁴